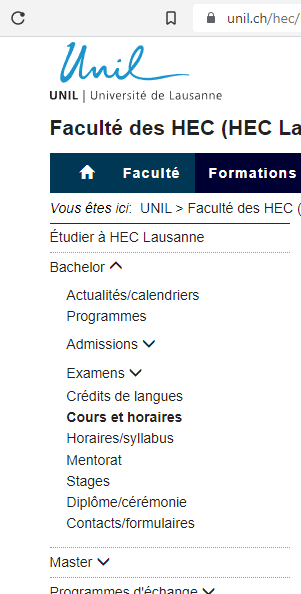
New Embeded Timetables
Please find Courses and timetables directly in your
Study program
Please find the Units charts now in Unisciences
Please find the Units charts now in Unisciences
![[logo_unil.png]](https://hecnet.unil.ch/medias/plone/lg14/logo_unil.png)